East-Asian ALMA Regional Center -- MAPS TO SCIENCE --

Maps to Science

原始惑星系円盤・原始星
1. 連続波イメージからダスト円盤の物理量を求める
2. 輝線キューブイメージからガス円盤の回転を知る
星形成領域
1. Dendrogram の利用
銀河
1. 近傍銀河: M100 CO 分子輝線データ
2. 遠方銀河: BR1202 [CII] 輝線データ
活動銀河核
1. (準備中)

原始惑星系円盤・原始星

原始惑星系円盤「連続波イメージよりダスト円盤の物理量を導出する」

ここでは作成されたイメージデータをもとにサイエンスを行うための例として、幾つかの典型的な解析を紹介します。

Jupyter Notebook 版スクリプト

ここで紹介する解析について Jupyter Notebook 形式の Python スクリプトも用意しました。 Jupyter Notebook 形式のファイルは以下からダウンロードできます。
ipynb ファイル (2024/02/09 改訂)
Jupyter Notebook 版スクリプトを実行するためには Jupyter Notebook がインストールされている必要があります。また、Python への CASA モジュールのインストールも必要になります (tarball でインストールされた CASA には対応しません)。 Jupyter Notebook 版スクリプトは例えば Google Colaboratory (※) 上で実行する事も出来ます (Google Colab 環境かを識別して自動的に CASA モジュールのインストールを行います)。
なお Jupyter Notebook 版スクリプトでは、以降で説明する様な解析をタスク viewer を使用しないで実現している点等で異なります。
※ Google Colaboratory (略称: Colab) は、Google の提供するブラウザから Python を記述、実行できるサービスです。 Jupyter Notebook 形式で書かれたスクリプトを読み込み、実行することが出来ます。

以降の解析は CASA 6.1 (Python 3) で動作確認しています。使用している CASA 関係のコマンドは CASA 5 (Python 2) でも問題ないはずですが、一部の Pythonコマンドが Python 2 で問題が起こるかもしれません。

イメージデータ

今回使用するデータは、ALMA で観測された原始惑星系円盤を持つ「HL Tau」の連続波イメージデータです。
ALMA Science Archive より、以下を検索してください。

Project code: 2018.1.01037.S
Source Name: HL_Tau

JVOのサイトからもイメージ FITS ALMA01424653_00_00_00.fits を直接ダウンロードできます。

FITS イメージ表示

タスク viewer を使用します。

# In CASA
viewer

または、

# In command line
% casaviewer &

で、viewerが起動します。

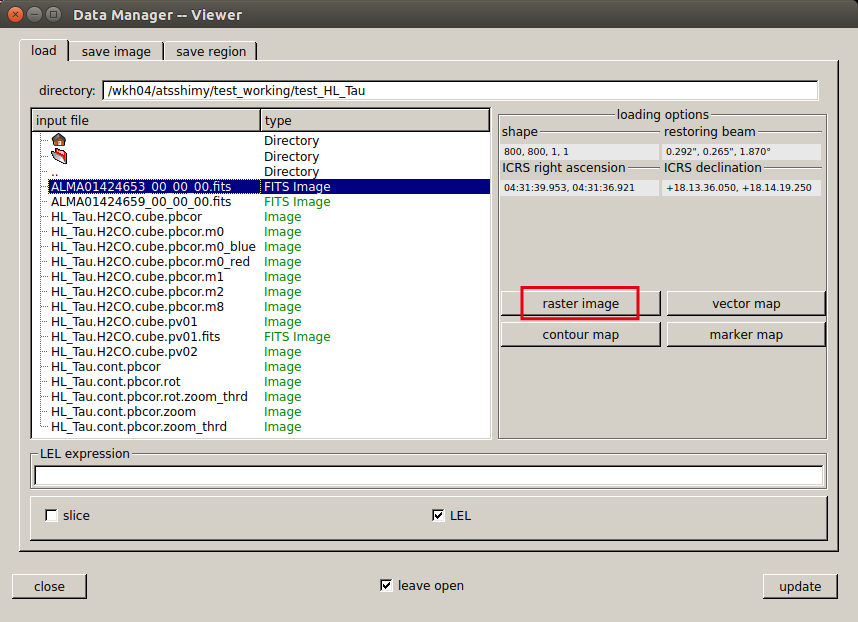"Viewer Display Panel" の他に、"Data Manager" というウインドウが開きます。ここで開きたいデータを選択し、"raster image" をクリックして下さい。 CASA 形式のイメージデータの他に、イメージ FITS ファイルも直接開くことが出来ます。

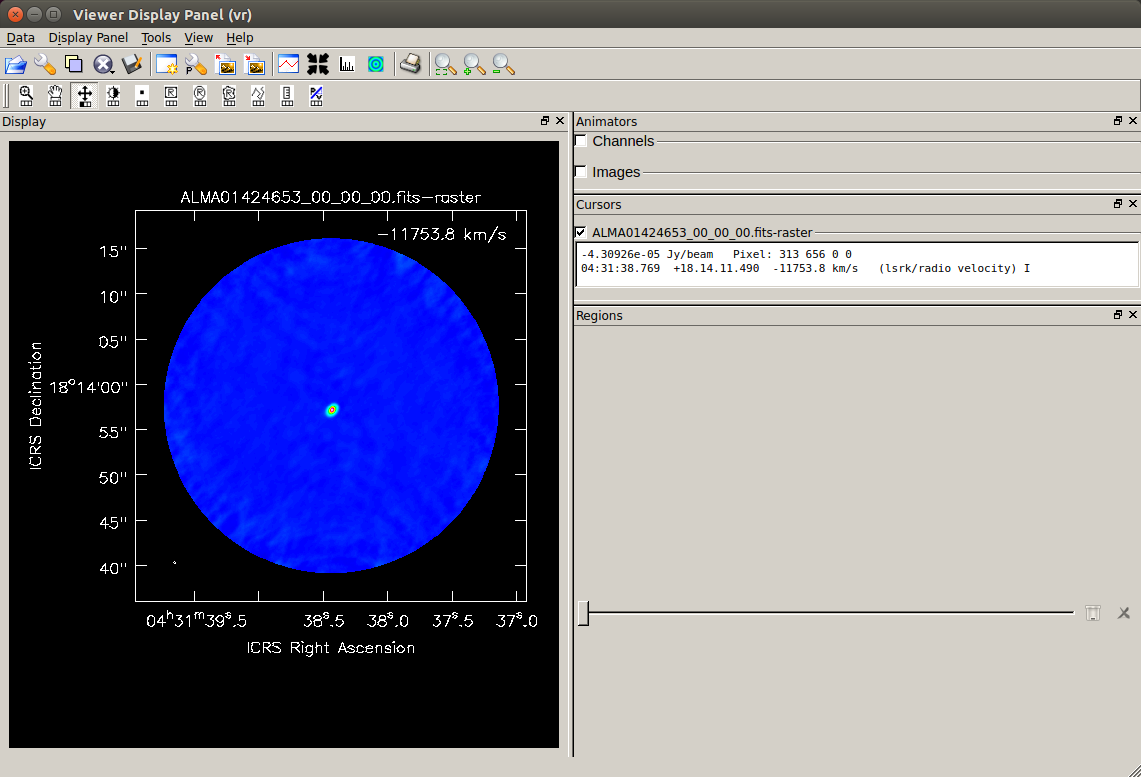"Viewer Display Panel" に、選択したイメージデータの画像が表示されます。

"Viewer Display Panel" 上部のパネルの各アイコンをクリックすると各種操作ができます。

拡大・縮小
移動 (画面上でマウスをドラッグ)
カラートーン変更 (画面上でマウスをドラッグ)

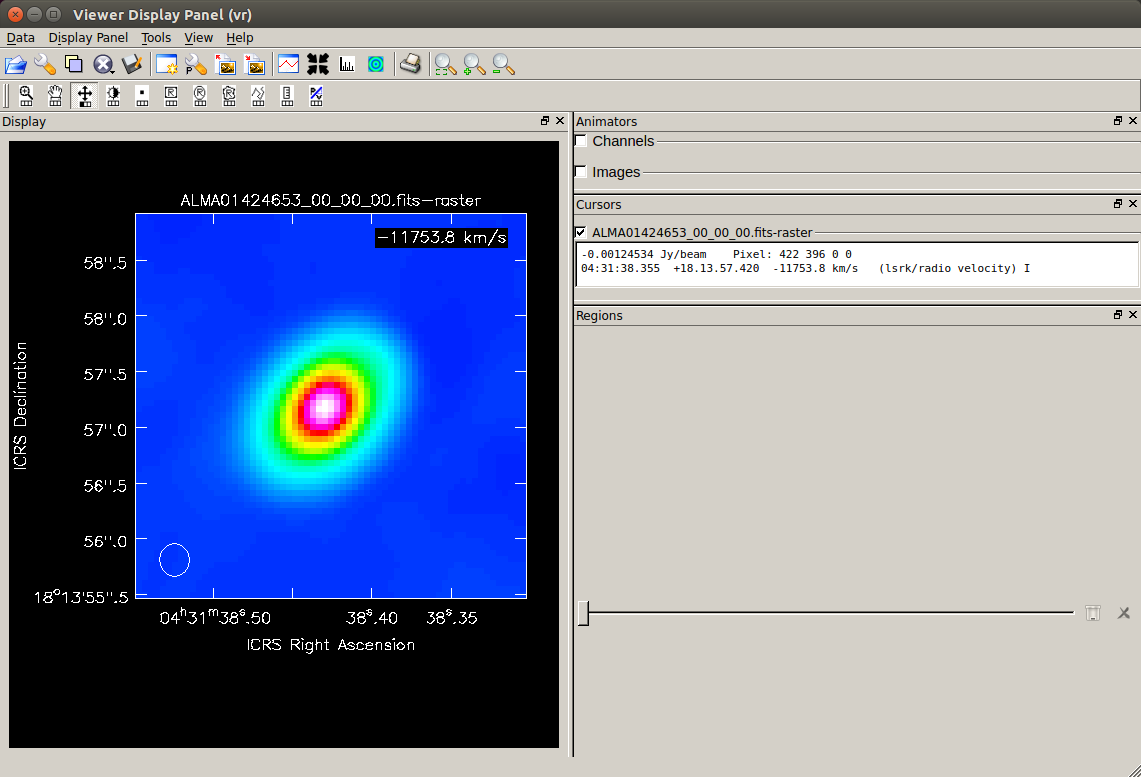拡大した HL Tau の連続波イメージです。

viewer の扱い方については、CASA docs の "Viewing Images" のページも参考にして下さい。

イメージ FITS 読み込み

# In CASA
inimfits='ALMA01424653_00_00_00.fits'
imname  = 'HL_Tau.cont.pbcor'
importfits(fitsimage=inimfits, 
           imagename=imname, overwrite=True)

タスク importfits でイメージ FITS を CASA 形式の画像ファイルに変換しています。 fitsimage には入力イメージ FITS 名を、imagename には出力される CASA 形式のファイル名 (実体はディレクトリ) を指定します。

ヘッダーから合成ビームサイズ (及び観測周波数) を確認

# In CASA
imname = 'HL_Tau.cont.pbcor'
imhd_A_res = imhead(imname)
bmaj  =imhd_A_res['restoringbeam']['major']['value']
bmajut=imhd_A_res['restoringbeam']['major']['unit']
bmin  =imhd_A_res['restoringbeam']['minor']['value']
bminut=imhd_A_res['restoringbeam']['minor']['unit']
bmpa  =imhd_A_res['restoringbeam']['positionangle']['value']
bmpaut=imhd_A_res['restoringbeam']['positionangle']['unit']
print('Synthesized Beam:')
print(f'   Major Axis = {bmaj:.7f} {bmajut}')
print(f'   Minor Axis = {bmin:.7f} {bminut}')
print(f'   Pos. Angle = {bmpa:.7f} {bmpaut}')
cfreq =imhd_A_res['refval'][2]
frequt=imhd_A_res['axisunits'][2]
if frequt == 'Hz':
    cfreqgh = cfreq/10**(9)
    print(f'Observing Frequency = {cfreqgh:.6f} GHz')
else:
    print(f'Observing Frequency = {cfreq:.1f} {frequt}')

Synthesized Beam:
   Major Axis = 0.2922270 arcsec
   Minor Axis = 0.2649764 arcsec
   Pos. Angle = 1.8701019 deg
Observing Frequency = 235.541305 GHz

イメージデータのヘッダーから合成ビームサイズが確認できます。タスク imhead を使用し、Python の辞書オブジェクトとして様々な情報が読み込まれます。これにより、ビームサイズの他に、イメージデータの各座標/周波数軸値・ピクセル間隔・ピクセル数なども確認できます。また、上記では観測周波数についても確認しています。

イメージ RMS (及び連続波放射ピーク) を確認

# In CASA
imname = 'HL_Tau.cont.pbcor'
stats1=imstat(imagename=imname, region='box[[260pix,265pix],[360pix,535pix]]')
stats2=imstat(imagename=imname, region='box[[440pix,265pix],[540pix,535pix]]')
imgrms=(stats1['rms'][0]+stats2['rms'][0])/2
print(f'RMS [mJy/beam] of {imname} : {imgrms*1000:.7f}')

RMS [mJy/beam] of HL_Tau.cont.pbcor : 0.4689696

さらに、

# In CASA
imname = 'HL_Tau.cont.pbcor'
ctx=400 ; cty=400 # center pixs
stats1=imstat(imagename=imname, 
          region='annulus[['+str(ctx)+'pix,'+str(cty)+'pix],[4.5arcsec,14.0arcsec]]')
imgrms=stats1['rms'][0]
print(f'RMS [mJy/beam] of {imname} : {imgrms*1000:.7f}')
stats2=imstat(imagename=imname, 
          region='circle[['+str(ctx)+'pix,'+str(cty)+'pix],4.5arcsec]')
imgmax=stats2['max'][0]
print(f'Max [mJy/beam] of {imname} : {imgmax*1000:.7f}')

RMS [mJy/beam] of HL_Tau.cont.pbcor : 0.4748368
Max [mJy/beam] of HL_Tau.cont.pbcor : 136.6068870

タスク imstat で、パラメータ region で指定された範囲内のイメージ RMS やピーク値などの統計量を計算しています。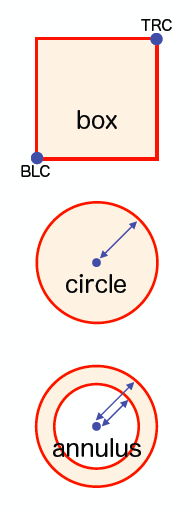

領域 "region" として、

"box" は BLC (bottom left corner; 左下), TRC (top right corner; 右上) を設定して四角形領域を指定します。
"circle" は中心位置と半径を設定して円形領域を指定します。
"annulus" はリング状の領域を指定でき、中心位置とリングの内側・外側の半径を設定します。検出天体を避けて RMS 等を求めるのに便利です。

region の指定方法について、詳しくは CASA docs の "Region File Format" をご覧ください。

イメージ RMS (ノイズの大きさ) を測るときは、天体からの放射のない領域で測定する様にします。上記では、"box" で天体からずらして四角形領域を指定したり、"annulus" で天体を取り囲むリング領域を指定したりしています。

求められた統計量は Python の辞書オブジェクト形式として読み込まれ、RMS の他にフラックス密度の最大値&最小値 (及びその位置)・合計・平均なども知る事が出来ます。
全ての統計量を表示したい場合は、先のコマンド実行後に

# In CASA
print(stats1)

としてください。

これらの統計量は viewer 上でも、region の指定に制限がありますが、簡単に確認することが出来ます。

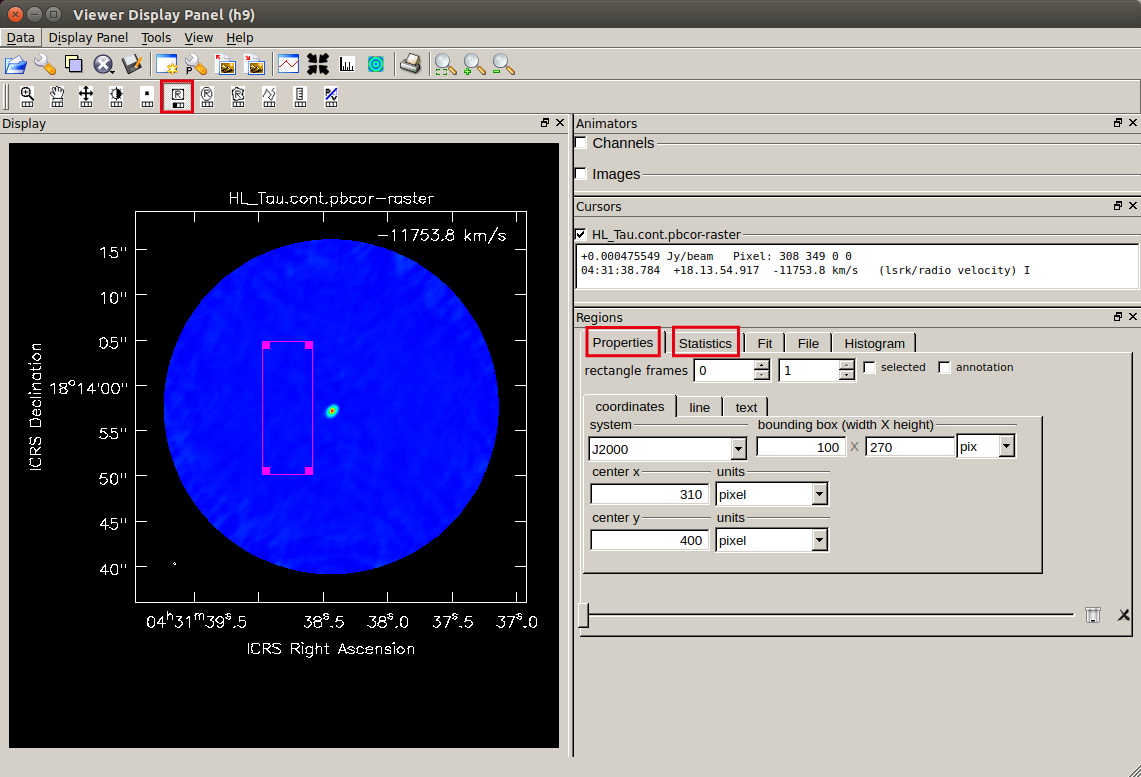連続波放射のない領域を、四角形領域選択ボタン (

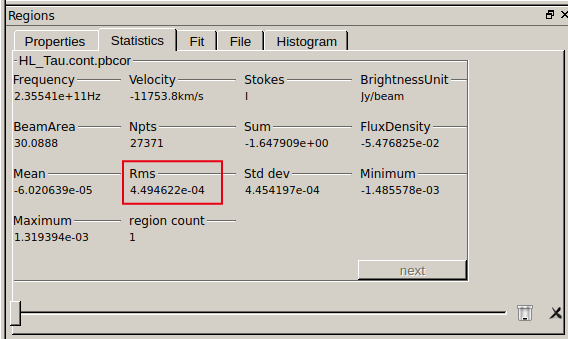の一番左) をクリックし、画像上でマウスをドラッグする事によって region を指定できます。詳細な領域設定は右側の "Regions" から "Properties" タブを開いて指定することもできます。

region を指定した後、"Statistics" タブを開くと、選択した領域内の RMS を含む統計量を確認することが出来ます。

天体の連続波放射を取り囲む region を選択すれば、ピークのフラックス密度などが分かります。

だたし、viewer で統計量を求める場合、周波数 (速度)チャンネルは表示されている 1 channel のみに対応し、領域設定は四角形・楕円形 (ただしいずれも回転はなし) 領域と、ポリゴンでの領域指定のみが可能です。

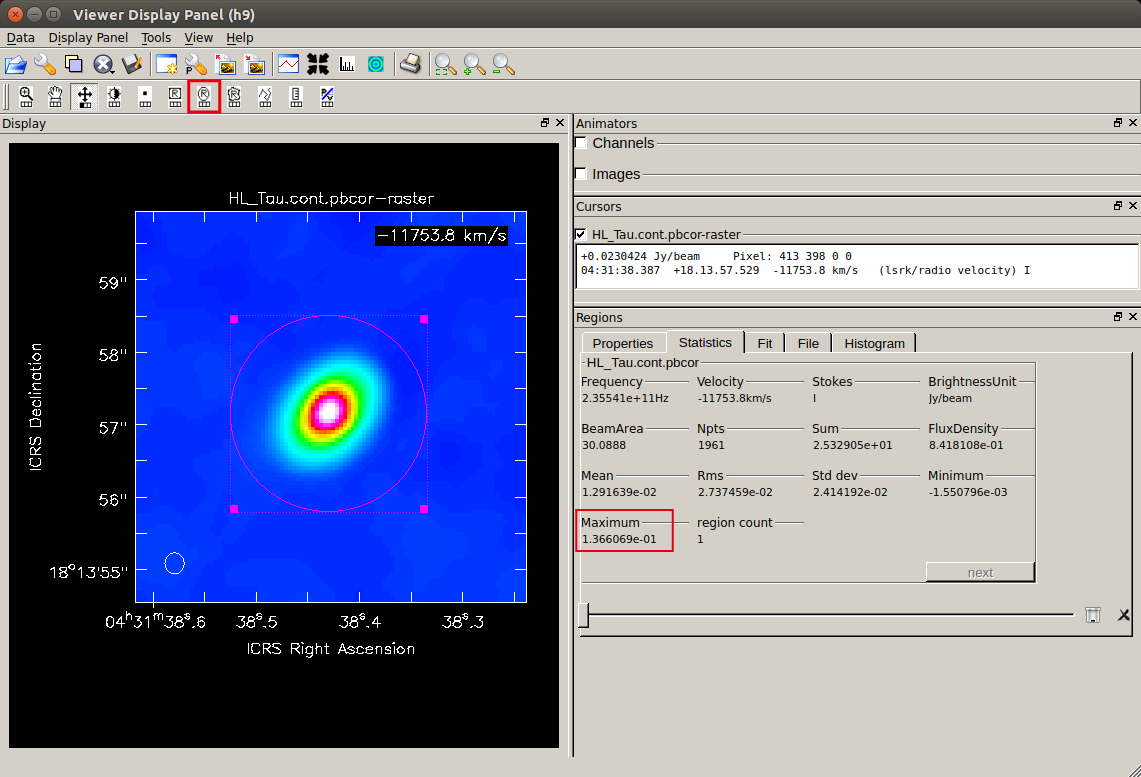
2 次元ガウシアンフィットによる原始星の位置推定

まず、viewer によるガウシアンフィットの方法を説明します。以下の手順で操作します。

viewer でイメージを読み込む
天体が分かる様に拡大表示・位置調整
対象の天体を取り囲む様に region を指定
右下の "Regions" から "Fit" タブを開き "gaussfit" をクリック

"Fit" タブに以下の様なフィッティングの結果が表示されます。

Ra_ICRS, Dec_ICRS : 中心位置 (絶対座標)
Xcen, Ycen : 中心位置 (pixel)
W-Majorax, W-Minorax : 長軸・短軸の FWHM (arcsec 等)
I-Majorax, I-Minorax : 長軸・短軸の FWHM (pixel)
IntegrFlux : トータルフラックス (Jy)
PeakFlux : ピークフラック密度 (Jy/beam)

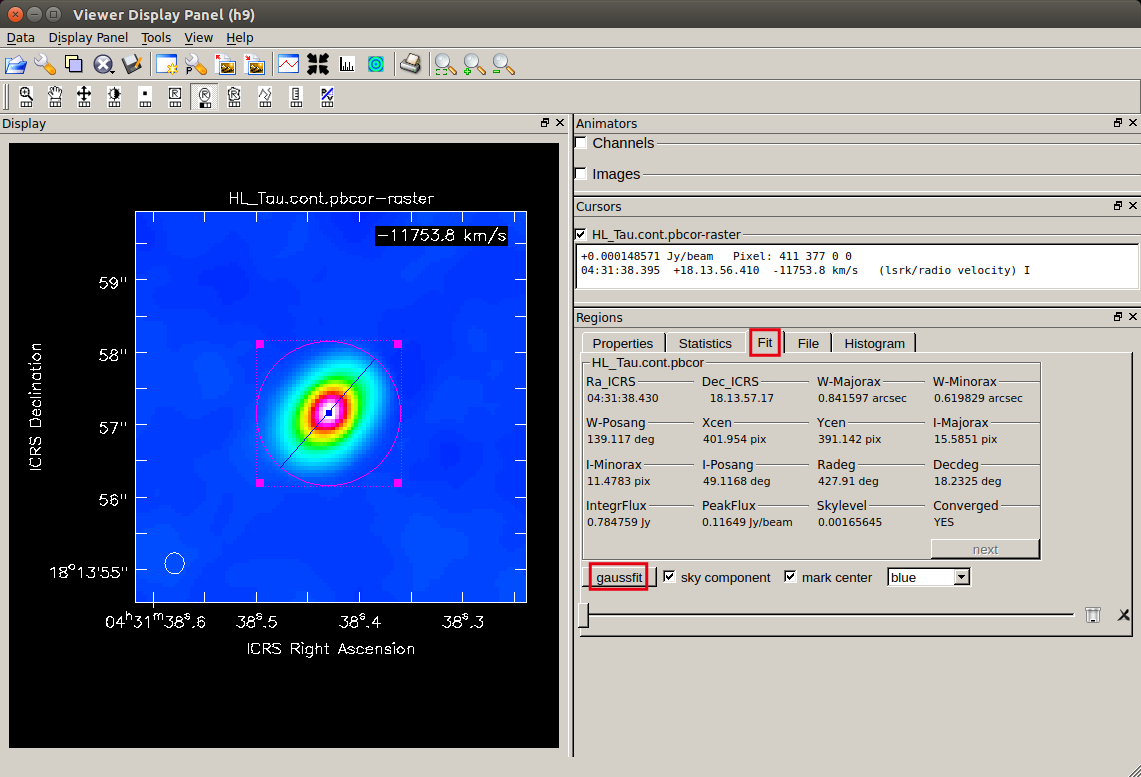また、画像上に中心位置と、長軸の向きが直線で表されます。

ガウシアンの中心位置から、原始星の位置を推定出来ます。中心位置の結果を、原始星 (HL Tau) の座標と比較してみてください。

以上を CASA のコマンドラインから行うと以下の様になります。あらかじめ viewer で天体の中心位置の pixel 値を大雑把に調べ、フィティングの初期値として ctpix, ctpiy で指定してください。

# In CASA
import math
imname = 'HL_Tau.cont.pbcor'
ctpix = 402 # pix
ctpiy = 391 # pix
xfit_B_res = imfit(imname,
                region = 'circle[['+str(ctpix)+'pix,'+str(ctpiy)+'pix],1.5arcsec]',
                newestimates = imname+'.imfit_estimates',
                logfile = imname+'.imfit_log')
xfit_B=xfit_B_res['results']['component0']
Flux  =xfit_B['peak']['value']                   ; FluxUn=xfit_B['peak']['unit']
Gmajor=xfit_B['shape']['majoraxis']['value']     ; GmajUn=xfit_B['shape']['majoraxis']['unit']
Gminor=xfit_B['shape']['minoraxis']['value']     ; GminUn=xfit_B['shape']['minoraxis']['unit']
Gpa   =xfit_B['shape']['positionangle']['value'] ; GpaUn =xfit_B['shape']['positionangle']['unit']
xxx1 = math.degrees(xfit_B['shape']['direction']['m0']['value'])
yyy1 = math.degrees(xfit_B['shape']['direction']['m1']['value'])
print('Gaussian fit :')
print("   Peak flux = %6.4f %s, FWHM = %6.4f %s x %6.4f %s (PA = %6.4f %s)" 
            % (Flux,FluxUn,Gmajor,GmajUn,Gminor,GminUn,Gpa,GpaUn))

Gaussian fit :
   Peak flux = 0.1164 Jy/beam, FWHM = 0.8656 arcsec x 0.6385 arcsec (PA = 138.9841 deg)

フィティングにはタスク imfit が使われています。 2 次元ガウシアンフィットの結果から、楕円ガウシアンのピークフラックス密度と長軸・短軸の半値全幅 (FWHM)・位置角 (PA) が求められています。フィッティングの結果は Python の辞書オブジェクト形式として読み込まれ、上記の他に多くのパラメータを確認する事が可能です。

長軸方向にスライスしたフラック密度分布

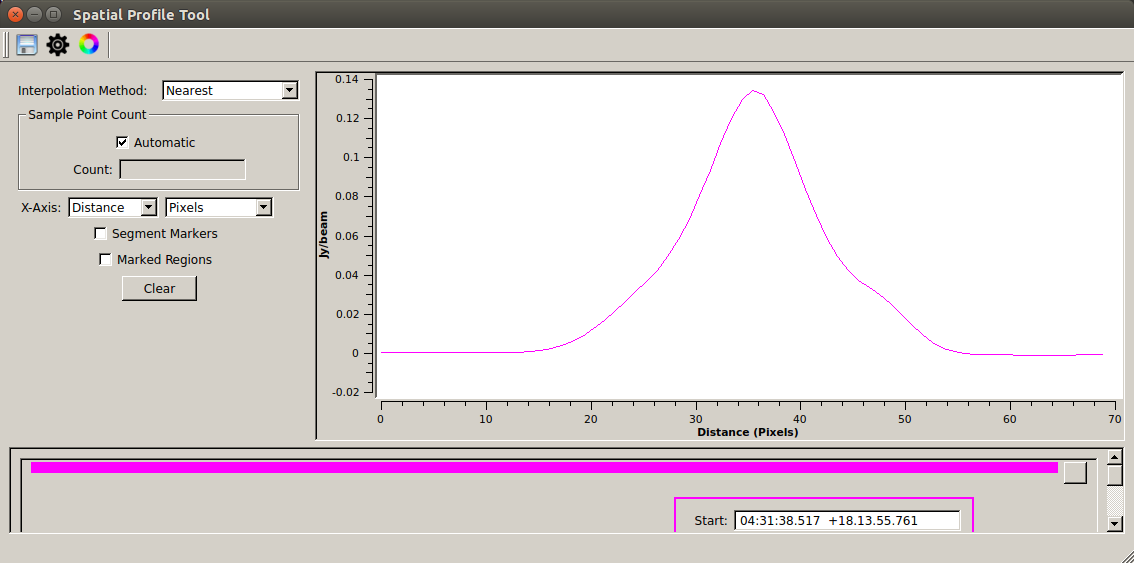
ガウシアンフィットで得られた中心位置と位置角 PA を基準に、長軸方向にスライスしたフラックス密度プロファイルを作成します。

タスク viewer を使って簡単に調べることが出来ます。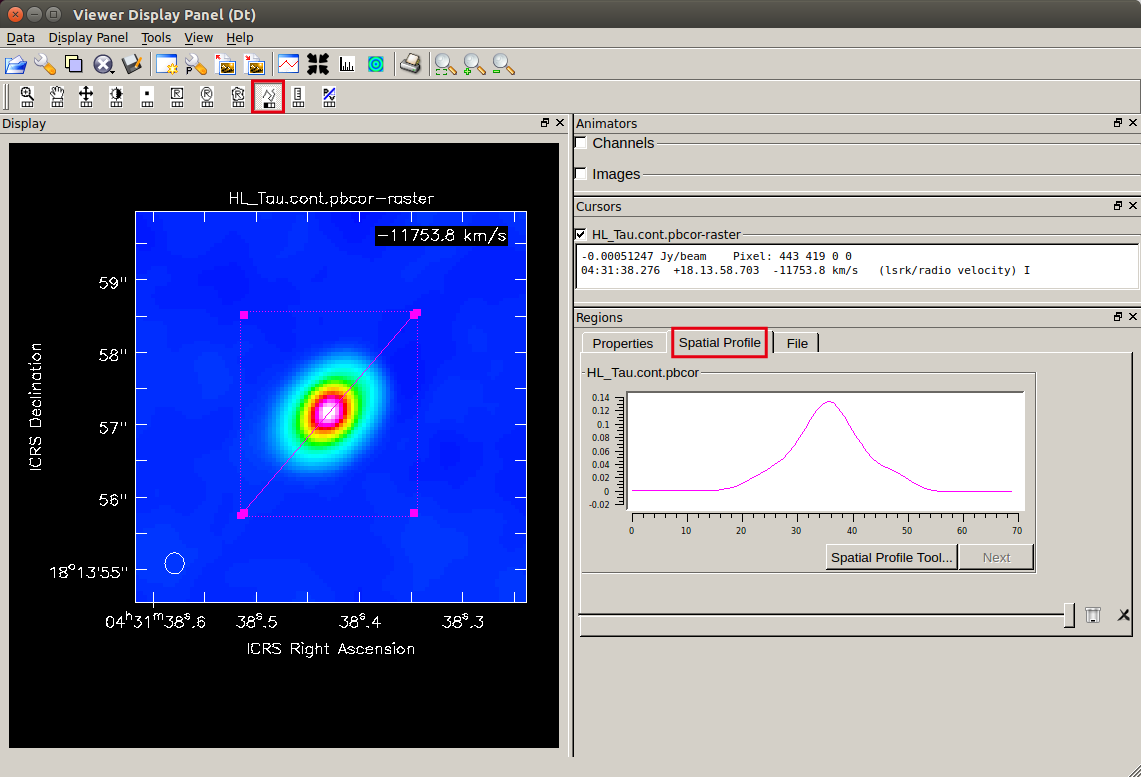

手順は、

イメージを読み込む
対象天体を拡大表示・位置調整
スライスする直線を指定 ( を選択した後、画面上で始点をクリック・終点をダブルクリック)
右下の "Regions" から "Spatial Profile" タブを開くと、指定した直線に沿ったフラック密度分布が表示される

このフラックス密度プロファイルから、実際には単純なガウシアンではなく、ピークの両側に緩やかに広がる成分があるのが分かります。この部分が円盤の成分と考えられます。

また、以下に CASA Toolkit を使ってフラックス密度プロファイルをテキストへ書き出す方法を紹介します。位置を厳密に指定したい場合はこちらも試してみて下さい。
前述の 2 次元ガウシアンフィットで得られた結果を参考に、天体の中心位置の pixel 値を pixx1, piyy1 で指定し、Gpa にはスライスする方向の位置角 PA (Position Angle) (円盤の位置角 PA と同じで良いでしょう) 、hspp にはスライスする長さを pixel で指定します。 cont_majaxis_profile.csv という csv (テキスト) ファイルに書き出されますので、グラフ作成ソフト等を使ってプロファイルを作成して下さい。

# In CASA
import math
import numpy as np
imname = 'HL_Tau.cont.pbcor'
pixx1= 402 # pix
piyy1= 391 # pix
Gpa = 138.98 # PA (deg)
hspp=60 # pix
blcx=int(np.round(pixx1-hspp/2.*math.cos(math.radians(Gpa-90.))))
blcy=int(np.round(piyy1-hspp/2.*math.sin(math.radians(Gpa-90.))))
trcx=int(np.round(pixx1+hspp/2.*math.cos(math.radians(Gpa-90.))))
trcy=int(np.round(piyy1+hspp/2.*math.sin(math.radians(Gpa-90.))))

ia.open(infile=imname)
rec = ia.getslice(x=[blcx,trcx], y=[blcy,trcy], npts=hspp)
ia.close()

path_w = 'cont_majaxis_profile.csv'
rec_dp = [str(n)+','+str(m) for n,m in zip(rec['distance'],rec['pixel'])]
with open(path_w, mode='w') as f:
    f.write('\n'.join(rec_dp))
f.close()

連続波イメージの 5σ 以上の放射よりダスト円盤の半径・傾き推定

連続波イメージの 5σ 以上の放射を持つ範囲をダスト円盤の見かけの大きさと考えて、長軸・短軸径からダスト円盤の半径・傾きを求めます。

viewer による空間スケールの測り方を説明します。
まず、viewer で 5σ 放射領域をコントアで表示します。連続波イメージを "raster image" で表示させた後、同じイメージデータを "contour map" で開いて下さい。

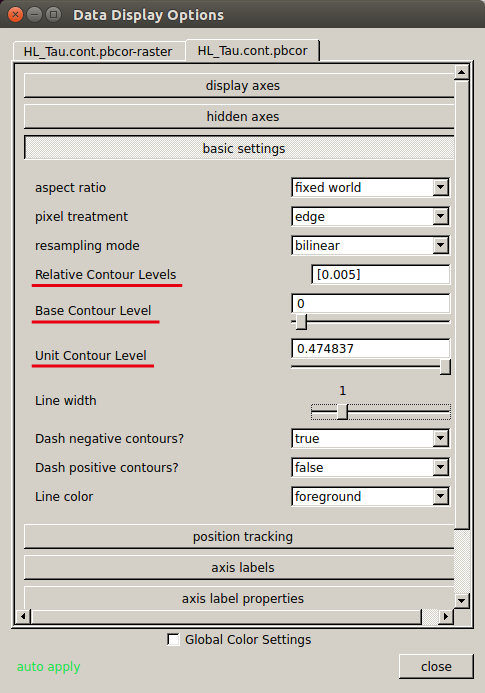"Data Display Options" (

アイコン) を開いてコントア表示しているイメージのタブを選択してから、"basic settings" をクリックしてパラメータリストを表示、

Relative Contour Level=[0.005]
Base Contour Level=0
Unit Contour Level=RMS(mJy/beam)

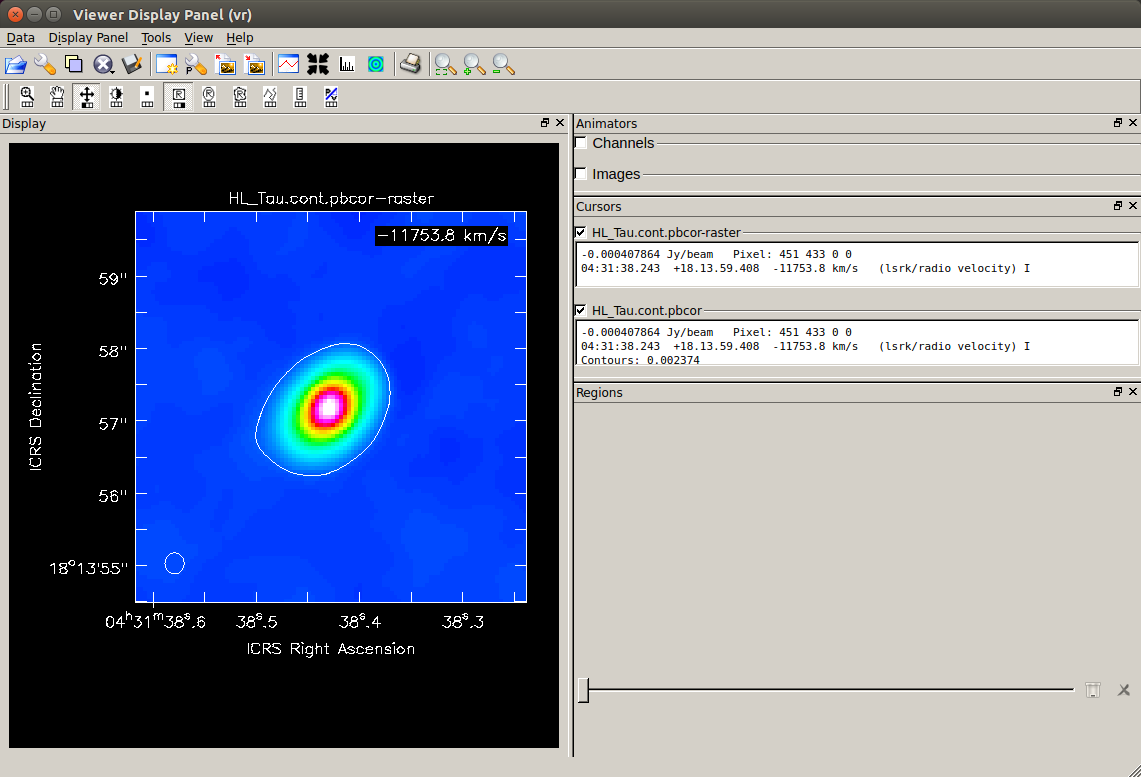と指定すると、5σ レベルのみにコントアが引かれます。RMS には先に調べたイメージ RMS を指定して下さい。

カラーイメージに重ねて、5σ レベルにラインが引かれたのが分かります。

この画像をもとに、5σ 以上の放射領域の長軸・短軸径を測ります。

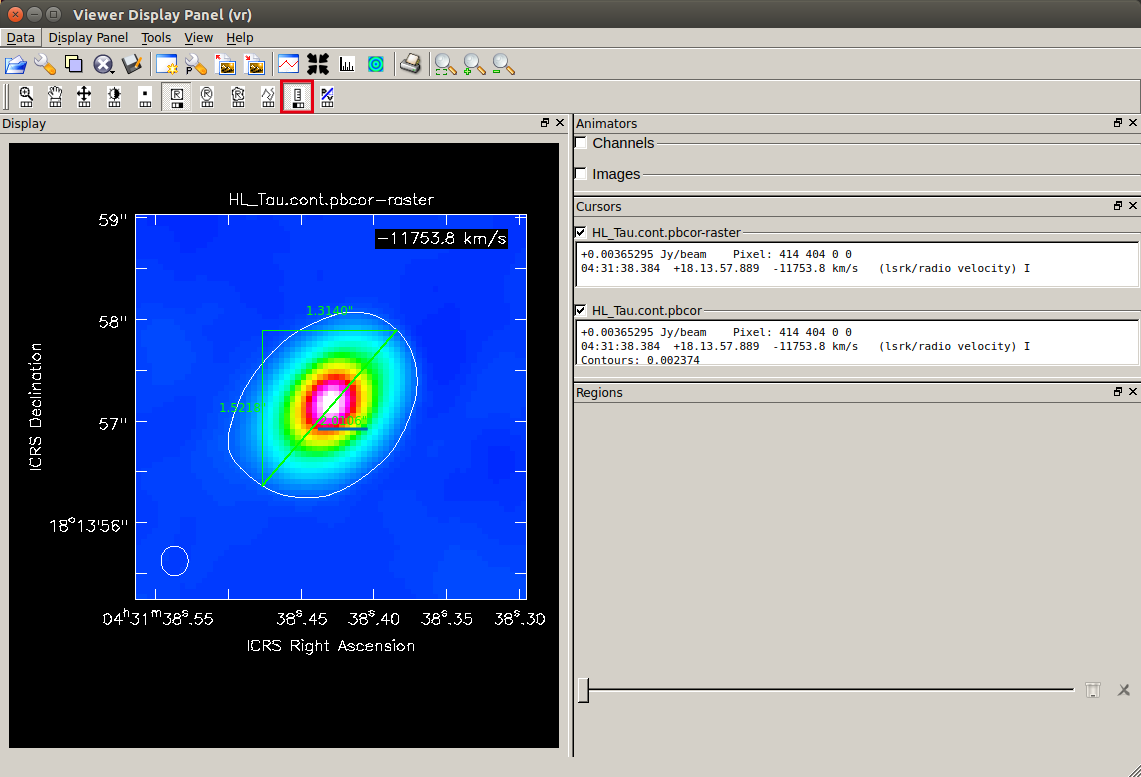"物差しツール" (

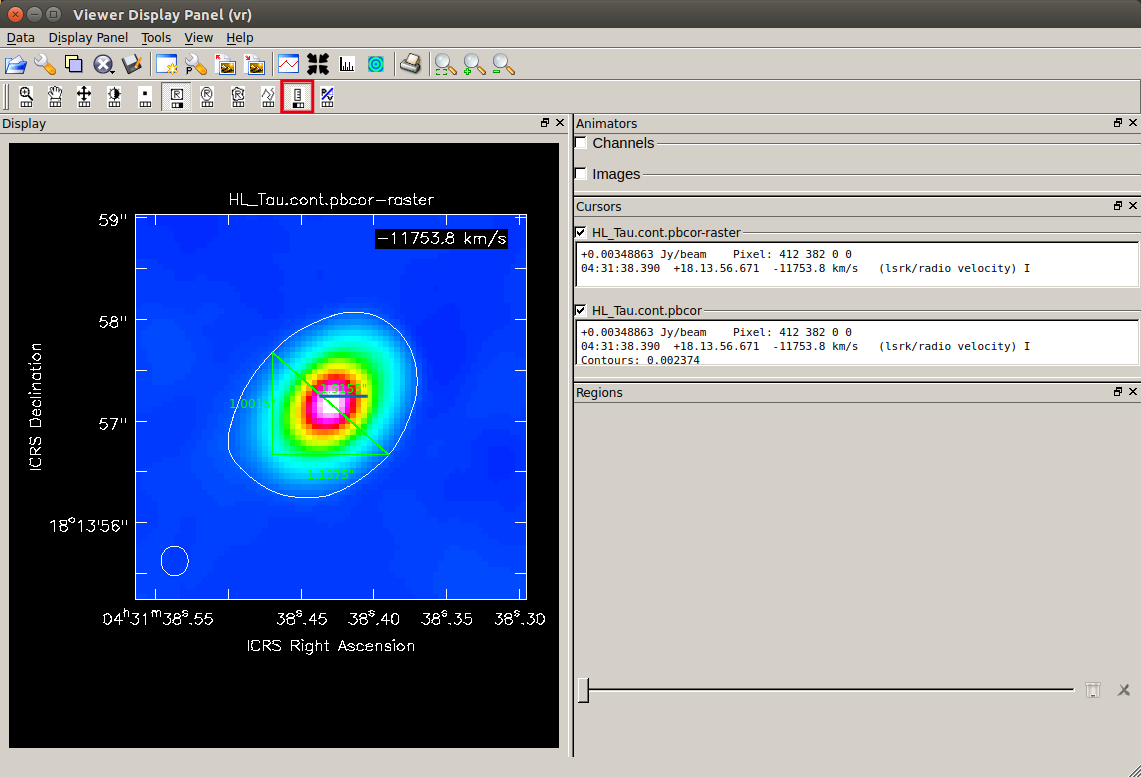アイコン) をクリックした後、イメージ上で測りたい範囲に合わせてマウスをドラッグして下さい。ドラッグした範囲のスケールが [arcsec] で表示されます。こちらは長軸方向で、2.0106" と表示されています。

こちらは短軸方向で、1.5155" と表示されています。

上記で得られた長軸・短軸の大きさより、ダスト円盤の半径・傾きが以下の様に推測されます。

# In CASA
import math
majax = 2.0106 # arcsec
minax = 1.5155 # arcsec

au  = 1.49597870700*10**(11) # m/AU
pc  = 3.085677581*10**(16)   # m/pc
dist= 140. # pc @ HL Tau
radi=dist*(pc/au)*math.tan(math.radians(majax/3600))/2
incl=math.degrees(math.asin(minax/majax))
print(f'Disk radius & inclination = {radi:.4f} AU, {incl:.4f} deg')

Disk radius & inclination = 140.7420 AU, 48.9167 deg

厚みが十分薄い軸対称な円盤を斜めから見ていると仮定すると、見た目の長軸径が円盤の直径に相当します。また、円盤の傾き (inclination: face on より) i は、軸比より

の関係になり、これらの関係からダスト円盤の半径・傾きが求められます。半径の物理的な長さ r は、視直径 Θ・天体までの距離 D とすると

の関係にあるとして計算しています。また、ターゲット天体 HL Tau までの距離は 140 [pc] と仮定しています。

以上を CASA のコマンドラインから行うと以下の様になります。

# In CASA
import math
import numpy as np
Gpa = 138.98 # PA (deg)
imgrms = 0.4748368 # RMS (mJy/beam)

imname = 'HL_Tau.cont.pbcor'
imname0 = imname +'.rot'
rotpa = -Gpa+90.
ia.open(infile=imname)
imr = ia.rotate(outfile=imname0, pa=str(rotpa)+GpaUn, overwrite=True)  
imr.done()  
ia.close()

imname1 = imname0 +'.zoom_thrd'
nsigma = 5.0               # σ threshold
threshold = (imgrms/1000)*nsigma
ctx=400 ; cty=400 ; iwd=60 # center pixs & image width
blcx=int(ctx-iwd/2) ; trcx=int(ctx+iwd/2)
blcy=int(cty-iwd/2) ; trcy=int(cty+iwd/2)
box1=','.join([str(blcx), str(blcy), str(trcx), str(trcy)])
os.system('rm -rf '+imname1)
immath(imagename=[imname0],
       expr='IM0[IM0>%f]'%threshold,
       box = box1,
       outfile=imname1)

box2=','.join([str(0), str(0), str(iwd-1), str(iwd-1)])
imv_res = imval(imagename=imname1, box=box2)
imv_data = imv_res['data']
imv_mask = imv_res['mask']
imv_dt_tp = imv_data.transpose(1,0)
imv_mk_tp = imv_mask.transpose(1,0)
np.putmask(imv_dt_tp, imv_mk_tp==False, "0")
xslice = imv_dt_tp.sum(0)
yslice = imv_dt_tp.sum(1)
nxpix = np.sum( np.where(xslice > 0, 1, xslice) )
nypix = np.sum( np.where(yslice > 0, 1, yslice) )

imhd_A_res = imhead(imname1)
incrx = abs(math.degrees(imhd_A_res['incr'][0])*3600)
incry = abs(math.degrees(imhd_A_res['incr'][1])*3600)
if nypix*incry >= nxpix*incrx:
    Gmajor = nypix*incry
    Gminor = nxpix*incrx
else:
    Gmajor = nxpix*incrx
    Gminor = nypix*incry
print(f'major/minor axes of 5 sigma area = {Gmajor:.4f} [arcsec] x {Gminor:.4f} [arcsec]')

au  = 1.49597870700*10**(11) # m/AU
pc  = 3.085677581*10**(16)   # m/pc
dist= 140. # pc @ HL Tau
radi=dist*(pc/au)*math.tan(math.radians(Gmajor/3600))/2
incl=math.degrees(math.asin(Gminor/Gmajor))
print(f'Disk radius & inclination = {radi:.4f} AU, {incl:.4f} deg')

上記では、指定した位置角 PA (Position Angle) 分だけイメージを回転させ、5σ 以上のフラックス密度を持つ領域を切り出したイメージを作成し、 X 方向・Y 方向にデータのあるピクセルの個数から長軸・短軸径を推定しています。

連続波イメージの 5σ 以上の放射からトータルフラックスを算出、ダスト質量を推定

以下の様にタスク immath を使って、5σ レベル閾値以上の領域を切り出したイメージを作成できます。さらに、5σ 以上の連続波マップからタスク imstat によりトータルフラックスが算出できます。
imgrms はイメージ RMS です。先に求めた値を使いましょう。なお、以下では 5σ レベル閾値とともに円盤中心付近を切り出しています。また、閾値を 5σ から変えたいときは nsigma を変更して下さい。

# In CASA
imname = 'HL_Tau.cont.pbcor'
imname2 = imname+'.zoom_thrd'
imgrms = 0.4748368 # RMS (mJy/beam)
nsigma = 5.0               # σ threshold
threshold = (imgrms/1000)*nsigma
ctx=402 ; cty=391 ; iwd=60 # center pixs & image width
blcx=int(ctx-iwd/2) ; trcx=int(ctx+iwd/2)
blcy=int(cty-iwd/2) ; trcy=int(cty+iwd/2)
box3=','.join([str(blcx), str(blcy), str(trcx), str(trcy)])
os.system('rm -rf '+imname2)
immath(imagename=[imname],
       expr='IM0[IM0>%f]'%threshold,
       box = box3,
       outfile=imname2)
stats=imstat(imagename=imname2)
imgflx=stats['flux'][0]
print(f'Total Flux [Jy] of {imname2} : {imgflx:.7f}')

Total Flux [Jy] of HL_Tau.cont.pbcor.zoom_thrd : 0.8354889

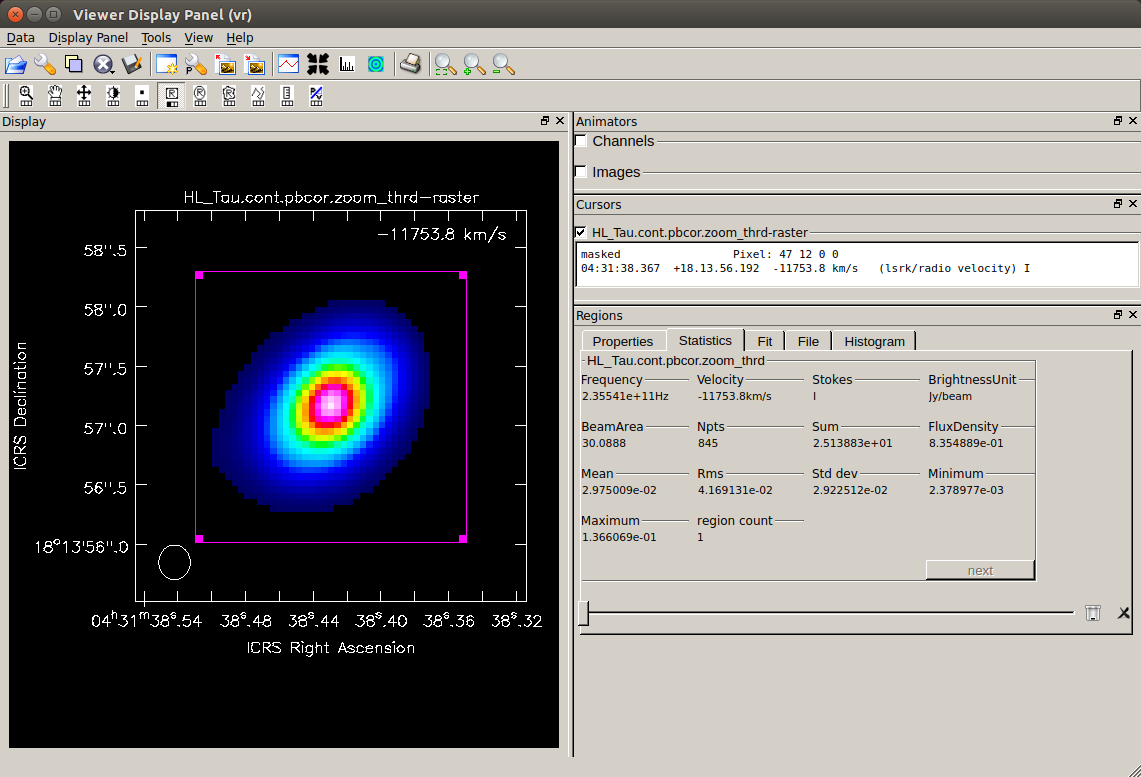ここで作成された 5σ レベルマップを viewer で表示すると右の様になります。上記の値は、この画像内部の総連続波フラックスを求めています。
viewer 上でトータルフラックスを確認するには、region として全体を選択し "Statistics" タブを開いて "FluxDensity" の値を見てください。

求められた連続波放射の起源がダストからの熱放射であり、かつ放射が光学的に薄いと仮定すると、ここで求めた連続波トータルフラックスより円盤のダスト質量 M_dust は以下の式から求められます。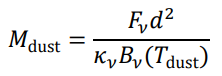

ここで F_ν がトータルフラックス、d は天体までの距離、T_dust はダストの温度を表します。 B_ν (T_dust) はダスト温度 T_dust におけるプランク関数 (黒体放射の放射エネルギー) を表し、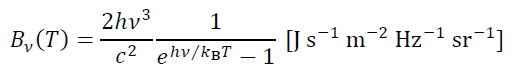

の式で示されます。
また、κ_ν はダストのオパシティ (opacity・吸収係数) を表し、ここでは

としています (Beckwith et al. 1990)。より一般的には κ_ν は周波数の指数関数 κ_ν ∝ ν^β で近似されますが、この式では β = 1 を仮定しています。オパシティ κ_ν は β を含めて不定性の大きな値であることにご注意下さい。 (一部の文献では、ガス-ダスト質量比を 100 と仮定して、ガス質量を含めたオパシティを使用している事にご注意下さい)
なお、HL Tau までの距離は d = 140 [pc]、ダスト温度は T_dust = 20 [K] を仮定しています。

# In CASA
import math
hhh = 6.626*10**(-34) # J*s   Planck constant
ccc = 2.998*10**(8)   # m/s   speed of light
kkb = 1.381*10**(-23) # J/K   Boltzmann constant
pcc = 3.087*10**(16)  # m/pc  parsec
Mso = 1.989*10**(30)  # kg    Solar mass
J2E = 10**(-26)       # 1 Jy = 10-26 W・m-2・Hz-1

# for HL Tau
dist = 140. # pc   distance
Tdust = 20. # K    dust temperature

imname = 'HL_Tau.cont.pbcor'
nu = imhead(imname)['refval'][2] # Hz  observing frequency
Fcont = imgflx        # Jy   continuum flux

# Planck function
Bpf = ( (2.*hhh*nu**3) / (ccc**2) ) / ( math.exp((hhh*nu)/(kkb*Tdust))-1 )
# dust opacity (Beckwith et al. 1990)
kap = 10*((nu/(10**9))/1000) / 10  # m^2 kg^-1
# dust mass (Mo)
Mdust = (Fcont*J2E*(dist*pcc)**2) / (kap*Bpf) / Mso
print(f'Dust mass on disk = {Mdust:.6f} Mo')

Dust mass on disk = 0.001313 Mo

以上の計算により、連続波放射のトータルフラックスより円盤のダスト質量を求めることが出来ます。

ページ先頭に戻る

Last Update: 2024.02.15